Romance in the upper half plane: The interplay between Modular forms and Hyperbolic geometry

Written by Bharath Krishna S and Ajin Shaji Jose

The origin of this article can be traced back to the previous semester at our University, where we had a course on Modular forms and Hyperbolic geometry. Upon getting introduced to these and exploring further, we could see that these two are very much inter related in many aspects and we went in search of that. Unfortunately, we couldn’t find many resources highlighting these connections, even as we could spot many resources covering these topics independently. Thus, we decided to compile a few things in this regard and this article is a result of that. We would like to focus more on the connections part and hence we won’t build these two concepts from scratch. However, we shall direct the reader to some useful resources where such information can be found and introduce briefly the concepts that need explanation as far as this article is concerned. This article gives  intuitive ideas, motivation and geometric understanding. In order to make it an expository article, some details, verification and proofs are omitted. Some basic knowledge of group theory, linear algebra, real and complex analysis and topology will help, even as it is not fully necessary to go further in this article. We begin with a short motivation on how these two branches of Math developed and what they are about.

Blasts from the past

Euclid's Elements was one of the earliest mathematical works which took an axiomatic approach to plane geometry where the whole theory is developed from five postulates and method of logical deduction. The fifth postulate also well known as parallel postulate was more bulky than its counterparts, so naturally mathematicians wondered if they could prove it from other four axioms. By efforts of Gauss, Bolyai, Lobachevsky and most importantly Beltrami, we now know that these efforts were futile ie. the parallel postulate is independent from rest of the axioms. Hyperbolic geometry is one of those geometries that grew out of the search to violate parallel postulate. One striking difference is that in usual Euclidean plane is that given a line and a point not on that line, there is a unique line passing through the given point parallel to given line (Playfair's axiom) whereas in hyperbolic plane, there are infinitely such parallel lines. While we study Euclidean geometry using Cartesian plane $\mathbb{R}^{2}$, we use different models to study Hyperbolic Geometry. Poincare half plane model is one such model. The underlying set is the upper half plane $\mathbb{H} \; = \; \{z \in \mathbb{C} \; | \;  \Im (z) > 0 \}$. Hence hyperbolic geometry is sometimes referred to as the geometry of the upper half plane. However the distance function we use is different from the usual Euclidean metric, which is the small spark, which ignites the field of Hyperbolic geometry. This gives rise to two entities playing the role of that played by a line segment in the Euclidean case. More precisely, we consider arcs of semi circles centered at the real axis as a way to measure distances in addition to vertical lines. This will further be explored towards the end of this article. One can do trigonometry, calculus, analysis and similar such things that we do in Euclidean case, in the hyperbolic set up  as well.  

 

Fig 1: Violation of Euclid's parallel postulate

With this, we switch to Modular forms. This is one of the most important concepts in modern day number theory. It originated as a concept in Complex analysis along with its closely related cousin - the automorphic forms -  during the 19th century. The use of modular forms became ubiquitous in number theory and counting problems as it started flourishing in the 20th century and some of the earliest examples of modular forms came out in connection with some counting problems. Various Mathematicians including but not limited to Ramanujan, Mordell, Hecke, Petersson, Taniyama and Shimura, Deligne, Serre and a lot of others who worked on the Fermat's last theorem, have contributed to the modern day theory of modular forms. This holds a special place in the proof of Fermat's last theorem as well. It is also used in theoretical physics as well. It is said that Mathematician Martin Eichler considered modular forms as a fundamental operation along with the already existing four operations in addition, subtraction, multiplication and division. This became quite popular in math discussion circles in the social media, when people commented that Ed Sheeran should name one of his albums as Modular forms.  Modular forms (defined over a congruence subgroup) are basically complex analytic functions defined on the upper half plane and satisfying a certain "invariance" condition corresponding to a specific group action (due to the congruence subgroup) and every modular form comes with a weight attached to it, thanks to certain kinds of "symmetry" relations that it satisfies. It can be shown that modular forms of a particular weight and over a congruence subgroup forms a vector space. With this motivation in mind, lets start exploring the connections now. 

 Fig 2: Some visuals of Modular forms which describe their fascinating symmetries

Lights, camera, ACTION!!!

We observe that $\mathbb{H}$, along-with the group $SL(2,\mathbb{Z})$  plays an important role in both of these branches by being the plane of action and as the title suggests, it is not surprising that the upper half plane and the action on it is the first connecting feature that we will encounter in this article. We are interested in "distance preserving" maps on $\mathbb{H}$. It turns out that these are precisely maps of the form $z \mapsto \frac{az+b}{cz+d}$ where $ad - bc =  1$ and $a,b,c,d \in \mathbb{R}$. We can describe these functions by an action of a group of matrices on $\mathbb{H}$ given by $\begin{pmatrix} a&b\\c&d \end{pmatrix}.z = \frac{az+b}{cz+d}$. These maps are called Mobius maps and this will turn up in definition of a modular form. The set of "distance preserving" maps which also preserves orientation, denoted by $PSL(2, \mathbb{R})$ consists of maps of the form  $z \mapsto \frac{az+b}{cz+d}$ where $ad - bc =  1$ and $a,b,c,d \in \mathbb{R}$. With the group action considered above, we may interpret it as elements of $SL(2, \mathbb{R})$. Though $SL(2, \mathbb{R})$ acts on $\mathbb{H}$, the action of  $SL(2,\mathbb{Z})$ on $\mathbb{H}$ is more interesting properties as we shall see. There is a natural topology on group of matrices which induces a topology on set of Mobius maps. So we can talk about discrete subgroups of group of "distance preserving" maps on $\mathbb{H}$. These are called Fuchsian groups. A very important example of a Fuchsian group is $PSL(2, \mathbb{Z})$ which is a subgroup of $PSL(2, \mathbb{R})$ where all the coefficients are integers. Naively speaking this group is the same as $SL(2,\mathbb{Z})$ in some sense . While modular forms primarily uses certain subgroups of $SL(2,\mathbb{Z})$ called the congruence subgroups, hyperbolic geometry basically uses a much higher class of groups namely the Fuchsian groups. Now, we come to the question of why is the upper half plane used in these contexts. The first crucial observation is that $\mathbb{H}$ comes with a natural  boundary $\partial \mathbb{H}$ in the form of the real axis $\mathbb{R}$ and an artificial point $\infty$. This becomes more apparent when you study the stereographic representation of complex plane $\mathbb{C}$. In the case of modular forms, this boundary contains special points called the cusps, which are involved in defining another notion called cusp form. But more importantly, cusps also help in finding the dimension of the vector space of modular forms of given weight. This process of finding this dimension involves the use of topology of the orbit space (basically identifying equivalent points under the action) of the action. The orbit spaces initially don't have nice properties to start with. But adjoining these points from the boundary does the job, which in turn facilitates this computation, using some techniques from geometry. As far as hyperbolic geometry is concerned, the fixed points of the above mentioned distance preserving maps are of particular interest and these maps are classified based on where the fixed points are found. Some of these fixed points are found in the boundary and those have connections with the limit set of the orbit of the action. Another crucial aspect of the action of $SL(2,\mathbb{Z})$ and some of its subgroups on $\mathbb{H}$ is that this action is "properly discontinuous". This is so powerful that this particular feature characterizes all the possible discrete subgroups of the set of isometries on $\mathbb{H}$. This highlights why we need the correct space and the group to act on it to get interesting results. 

 

Fig 3: The upper half plane with some points on marked on its boundary and a description of neighborhoods around them

 

 

By some specific maps, a correspondence can be established between $\mathbb{H}$ and the set $\mathbb{D}=\{q \in \mathbb{C} \mid   |q|<1\}$. Now whatever geometry we did in the upper half plane can be done in the unit disk $\mathbb{D}$. This comes in handy because we can see the entire space where our geometry happens. This beauty is captured in MC Escher's paintings, which are one of the most accurate descriptions of this type of geometry. In the case of modular forms, this transformation helps it to be depicted as a power series (called as $q$ series) in some neighborhood. This series expansion, particularly the coefficients contain much valuable information as far as number theorists are concerned. These coefficients sort of label the modular form, in the sense that it is most often enough to study its power series expansion even if we don't know the explicit function. In fact, some of the earliest known examples of modular forms were of the $q$ series type. In addition to being analytic in the upper half plane, modular forms are required to be analytic at the adjoined special points called cusps. The $q$ series expansion helps in proving the analyticity at cusps. Even as we described the importance of upper half plane and how it acts as a common feature between hyperbolic geometry and modular forms, one natural question to ask is if we can do the same kind of analysis by acting $SL(2,\mathbb{Z})$ on the lower half plane. Yes, that is possible due to the symmetry given by the real axis. But the signs should be taken care of as the points on the lower half plane are mere reflections of the points on $\mathbb{H}$ and vice versa. 

 

Fig 4: MC Escher's artworks which convey the idea of the geometry of the disk model

 

More on the action

Every action comes with two special type of sets, namely the stabilizer and the orbit, associated to every element of the set on which a group acts. The stabilizer of an element is a subgroup of the group and as the name suggests, it contains all the elements of the group that fixes the element under the group action. Orbit contains all possible translates of the given element by the group elements. One can define an equivalence relation on the elements of the set to get the orbit space of the action. In some special cases, as with the case of the action by congruence subgroups on $\mathbb{H}$, one can see the functions defined on $\mathbb{H}$ as functions defined on the orbit space of the action. One aspect of the action in our case, that we touched upon is the discontinuity. There are multiple equivalent definitions for a properly discontinuous action. This nature of action gives the required geometric structure (namely a Riemann surface structure) on the set of orbits, leading to a nice correlation between abstraction and geometry. Returning to fixed points, in the case of action by congruence subgroups, it is known that the stabilizer of a certain special kinds of points called the elliptic points, is a finite cyclic group. Elliptic points are those for which the stabilizer is non trivial, that is, it contains some matrix other than the identity (as trivially identity map fixes every point). The Riemann  surface structure also depends on the stabilizer. So far we have seen stabilizer which speaks about maps that fix a given point. Now one can also speak about the points in $\mathbb{H}$ that are fixed by a given map. A simple calculation shows that, any given map can have at most two fixed points in $\mathbb{H} \cup \partial \mathbb{H}$ as one solves for the equation $\frac{az+b}{cz+d}$=$z$ , which is a quadratic equation in $z$. Depending upon the discriminant of this quadratic, the roots can be purely real or complex. Thus, this gives the possibility of fixed points lying on the boundary. The maps are classified as hyperbolic, parabolic and elliptic based on the number of fixed points they have in the upper half plane and on its boundary. Further, it can be shown that the maps are essentially- dilation, translation and rotation, thereby explicitly giving the nature of the symmetry. Furthermore, Fuchsian groups generated by these three prototypes can be studied using their limit point sets and can be classified based on the cardinality of the limit sets. Thus, maps fixing points and points which get fixed by a map present an interesting connect between these two entities which flourish in the upper half plane. 

 

The geometry of the action: Enter the fundamental domains

The previous section has triggered the need to further study the geometry of the action. The upper half plane is a very big space and hence it is very hard to visualize it completely. Though one can always go to the unit circle to view the space fully, staying on in the upper half plane will present some advantages as well - one such being a simple complex contour integration to get the dimension of the space of modular forms. Also, we aim to get rid of the "extra" elements as well. More precisely, if one element can tell the details of another element under the action, why not consider only one of them.  Thus, we aim to find that part of $\mathbb{H}$ which is small enough, easy to deal with and contains all information about the action. The best thing to do in this context is to remove all those points equivalent to a particular point and keep only the non equivalent points in our space. We get on with finding a fundamental domain for $SL(2,\mathbb{Z})$. It can be proved with the use of division algorithm that the $SL(2,\mathbb{Z})$ is generated by two matrices, $$ T = \begin{pmatrix} 1&1 \\ 0&1 \end{pmatrix} \text{ and } S = \begin{pmatrix} 0&-1 \\ 1&0 \end{pmatrix}$$ Thus to study the action of an arbitrary element of $SL(2,\mathbb{Z})$, it is enough to study that of the generators. Now, the matrix $T$ corresponds to the map $z \mapsto z+1$, which is a translation by length 1. Thus, we can confine ourselves to a space between two parallel strips of width 1, for if the width is greater than 1, we can always use the map $T$ to find equivalent points. These two parallel vertical lines can pass through any point, but we would like to have zero at the centre. So we choose the region $\frac{-1}{2}<\Re (z)<\frac {1}{2}$. There is nothing specific about zero being the centre, because once we obtain a fundamental domain, translating it by length 1 gives another fundamental domain, which not only says that fundamental domain of $SL(2,\mathbb{Z})$ is not unique, but also highlights that one can start with any vertical strip of width 1. The point zero being the center is easy to work with because the map $S$ maps 0 to $\infty$. Now even as we can confine to the above given strip in $\mathbb{H}$ after applying $T$, we should consider the action of $S$ as well. Note that the map $S$ when explicitly stated, is $z \mapsto \frac{-1}{z}$. Thus, it is better to understand this by considering the unit circle. The points inside the unit circle satisfy $ |z|<1$ and hence $S$ maps these points outside the unit circle. Also the points outside the unit circle gets mapped to the interior. The points on the unit circle gets mapped among themselves. Considering all these we should either include the interior or exterior alone. Of course the boundary should be there. We choose the exterior of the circle. Thus, the set $$\{z \in \mathbb{H} \; | \; |z| > 1, |\Re (z)| < \frac{1}{2}  \}$$ is a fundamental domain of $SL(2,\mathbb{Z})$. All these can be formally proved. That is, we can show that no two points inside the above set are equivalent. Any element of $\mathbb{H}$ is equivalent to some point in this set. Also we would require our fundamental domain to be connected. Note that $T$ maps one of the vertical lines to another and the arc of the semi circle maps to itself under in an interesting way. The point $i$ maps to itself under $S$, while the half arc to the left of $i$ maps to the half on the right of $i$ and vice versa, albeit there is a change in the orientation. Thus, this motivates the need for a fundamental domain to come with a boundary identification. Similar study can be performed on any Fuchsian group $\mathcal{G}$ and its fundamental domain can be found. Dirichlet gave a systematic way to construct a fundamental domain $\mathcal{F}$ from a Fuchsian group and it is convex in the sense that any hyperbolic line segment with its endpoints in $\mathcal{F}$, lies in $\mathcal{F}$.

Fig 5: The standard fundamental domain of $SL(2,\mathbb{Z})$

 

Here we make a short note. At the beginning we mentioned that analogous concepts for polygons can be defined in the Hyperbolic world. Now, the above given fundamental domain is a hyperbolic triangle. In the hyperbolic world, due to a different notion of distance and the action of Mobius maps, we have two different entities (namely vertical lines and arcs of semi circles centered at the real axis) being sides of a polygon. These are technically known as geodesics, that is, in some sense, these are the possible types of curves on which the shortest distance between any given two points is attained. In the Euclidean geometry, we have only lines as geodesics. So we have observed that, there is a fundamental domain for $SL(2,\mathbb{Z})$, which is an hyperbolic polygon (however we have to tweak the definition a little bit to allow points and edges from boundary $\partial \mathbb{H}$ referred as ideal vertices and free edges). We can see that its boundary is a hyperbolic triangle with vertices $e^{i\frac{\pi}{3}}$ and $e^{i\frac{2\pi}{3}}$ and an ideal vertex $\infty$. Such a pattern can be observed for a few other congruence subgroups as well. Poincaré showed using an interesting and highly non trivial argument that under some hypothesis, aforementioned process can be reversed, that is from a convex hyperbolic polygon we can construct a Fuchsian group $\mathcal{G}$ for which the given polygon with its interior included is a fundamental domain. 

Coming back to the fundamental domain, it seems as if the part below the fundamental domain, consisting of the interior of the unit circle, may look as if it contains less points than the one above it. But in fact, it is just an illusion. It can be proved using the hyperbolic metric that, as we closer and closer to the boundary, we are actually travelling an infinite amount of distance. It is just that our eyes are too much adapted to see the Euclidean geometry and that makes this an illusion. 

Using a fundamental domain of a given Fuchsian group $\mathcal{G}$, we can tile the upper half plane by applying various maps from $\mathcal{G}$ on the given fundamental domain. Thus we get repeating copies of the fundamental domain which exhausts the whole of $\mathbb{H}$. 

 

Fig 6: Tiling $\mathbb{H}$ using the maps in $SL(2,\mathbb{Z})$

One crucial use of fundamental domain in modular forms is the computation of dimension formula for the space of modular form of weight $k$ over a congruence subgroup. For now, we will give a short overview of how it is done for $SL(2,\mathbb{Z})$. Let us consider the above mentioned standard fundamental domain of $SL(2,\mathbb{Z})$. As a modular form $f$ is analytic in the upper half plane, given a point on $z$  $\in$ $\mathbb{H}$, we can associate an integer to $f$ corresponding to the point $z$, namely the order of the zero of $f$ at $z$, meaning the multiplicity of the zero at $z$. Using the "symmetry" relations involved in the definition of modular forms, it can be observed that it is enough to study the zeros of $f$ in the standard fundamental domain to get information about the dimension. As a convention, we define the order of $f$ at $\infty$  to be the index corresponding to the minimum non zero coefficient in the $q$ series expansion of $f$, which we introduced in the initial paragraphs. With this set up in place, theorems from complex analysis ensures that there are only finitely many zeroes of $f$ inside the fundamental domain and that there is a neighborhood of $\infty$ (which is actually a region of $\mathbb{H}$ that lies above an appropriate horizontal line parallel to the real axis) such that $\infty$ is possibly the only zero of $f$ in that neighborhood. All this was possible courtesy the analyticity of $f$. Thus, the picture reduces to a compact region, given in the image below. We are looking to study about zeroes of a function in some compact region and one of the powerful theorems in complex analysis that is related to this is the argument principle. Note that we should choose our contour such that it doesn't pass through zeroes or poles. Using some basic contour (with the below given image as a contour) integration techniques (as illustrated in the following image), we can arrive at an interesting, non trivial and complicated looking identity called the valence formula, which involves $\frac{k}{12}$ on one side and an expression involving order of the zeroes on the other. The formula encodes information about the special types of points of $\mathbb{H}$ namely the elliptic points and the cusp of $SL(2,\mathbb{Z})$. In fact, the fundamental domain also gives some distinct picture to these points as one of the elliptic points is $i$ (the point about which the arcs in the domain gets identified) and the other is the two end points of the arc. The cusp is at $\infty$. The integration takes into consideration angles at these points to give some factor. For some specific values of $k$, it can be shown using the identity that there is no such $f$, implying the space of modular forms of weight $k$ is a trivial one. This factor of $\frac{k}{12}$ appears in the dimension formula, which can be proved separately for general values of $k$. Thus, finding the dimension of the space of modular forms of weight $k$ in some sense boils down to finding its zeroes in the standard fundamental domain. 

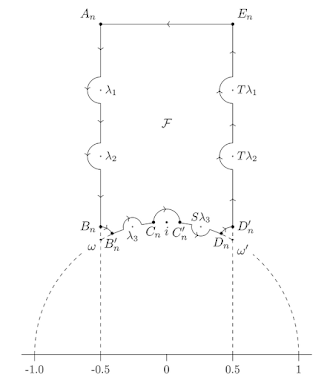
Fig 7: Contour for integration to find the valence formula for $SL(2,\mathbb{Z})$

We can adopt a similar approach to find the dimension the space of modular forms of weight $k$ over any other congruence subgroup of $SL(2,\mathbb{Z})$. We first find the corresponding valence formula which has some relation with the dimension formula. As in the case of $SL(2,\mathbb{Z})$, we can directly deduct the dimension of space of modular forms of certain weights over an arbitrary congruence subgroups, readily from the corresponding valence formula. In full generality, the dimension formula can be calculated by techniques using Riemann surface theory. The main advantage of this method is that we don't need to explicitly know a fundamental domain of the given congruence subgroup. This is more abstract and in hindsight it essentially works in the same way (though it is not explicit) as this method concerns with the meromorphic functions defined on the orbit space (which in some sense is the fundamental domain, albeit it is more abstract) and calculating the order of zeroes of these functions in the orbit space. Though it has been described in one line, the ideas involved in this shall require some more explanation.

The genesis of the hyperbolic world and more on modular forms

After having gone through the article thus far, we believe it may be tempting for the reader (after having seen some distinct features of the hyperbolic world) to think what differentiates Euclidean geometry and Hyperbolic geometry. According to Klein, geometry is study of a space (with a structure defined on it) and transformations on it which preserves the structure. In our case, the space is the upper half plane. The structure defined on it is the hyperbolic distance which involves a $\frac{1}{\Im(z)}$ factor, where $\Im(z)$ denotes the imaginary part of $z$. It can be shown that the magic of hyperbolic geometry arises due to this, in the sense that any function giving rise to this type of geometry on $\mathbb{H}$ must be a scalar multiple of $\frac{1}{\Im(z)}$. Naively speaking, as distances are measured using $\frac{1}{\Im(z)}$ factor, the areas are defined using a factor $\frac{1}{\Im(z)^2}$. The path lengths are defined using integrals involving the $\frac{1}{\Im(z)}$ factor. Similarly, the areas are defined using integrals involving $\frac{1}{\Im(z)^2}$ factor. 

 

Now how does these things connect to modular forms? As far as linear algebra is concerned, when we have a vector space, one tries to define some special type of functions called operators on the space and study their eigenvalues and eigenvectors. Hecke theory gives us ways to define operators on the space of modular forms and how to study their eigenvalues and eigenvectors. One nice way to find a basis of a vector space is using the eigenvectors of operators. To admit such a basis, the operators should satisfy certain properties and there should be an additional structure on the vector space called, the inner product. Petersson, using the above mentioned hyperbolic area formula, defined an inner product on the space of modular forms of weight $k$ to study the operators from Hecke theory. This inner product gave special properties to the operators which made it possible to find a nice basis for the space of modular forms, consisting of the eigenvectors of the operators, which are aptly named as eigenforms.

Final words...

Its time to sign off from quite a long exposition enjoying the interplay between two of the most interesting concepts in Mathematics. This has been a nice experience for us and hope we achieved our objective via this exposition so that the reader got benefited. Mathematics from time immemorial has continued to produce interesting and unexpected connections that come out of nowhere. Appreciating the connections not only makes us understand the concepts better, but also brings in nice analogies which can be used to explain concepts in a better way. As far as Mathematical research is concerned, connections build a bridge between different areas thereby increasing a possibility of more and more collaboration between seemingly unrelated areas. In our opinion collaboration is necessary to have a healthy environment in Mathematics and this surely helps. Connections also give rise to various practical applications like the case of prime numbers being used in security and cryptography. Also, these find applications within Mathematics as well - one example being the connection between modular forms (an analytic object) and elliptic curves (an algebraic object) which was the vital cog in proving the Fermat's last theorem. While connections seem ubiquitous after being heavily used, at the start to spot that connection might actually have been harder and non trivial, although a few connections might have been easier to spot. Another important aspect of these is to serve for the development of new areas in Mathematics. Historically the search and development of hyperbolic geometry predates that of modular forms. We feel that, it might have happened that people working on modular forms got some inspirations from hyperbolic geometry as well. One example of this is the definition of Petersson's inner product. Connections make different areas grow and prosper together and exploring their growth history helps us in understanding them better. One hopes that Mathematics and Mathematicians continue to throw up these interesting connections so that one day the graph with its vertices being the different branches of Math, becomes a complete graph. 

 

Acknowledgement

We thank the instructors of the Modular forms and Hyperbolic geometry courses that we had in our University and our peers who helped us with suggestions for improvement and had interesting discussions with us on this topic. 

References (with some suggestions)

1. Diamond, Fred, and Jerry Michael Shurman. A first course in modular forms. Vol. 228. New York: Springer, 2005.(a very good text for Modular forms - covering almost all relevant areas and introducing some prerequisites along the way as and when required)
2. Murty, M. Ram, Michael Dewar, and Hester Graves. Problems in the theory of modular forms. Springer Singapore, 2016.(a very good read to start with. It begins in an elementary way, with a good motivation and then progresses to further concepts)
3. Serre, Jean-Pierre. A course in arithmetic. Vol. 7. Springer Science & Business Media, 2012.(a classic compendium of some concepts used in modern day Number theory)
   
4. Katok, Svetlana. Fuchsian groups. University of Chicago press, 1992.(a classic for Hyperbolic geometry)
   
5. Helena Verill's fundamental domain drawer https://wstein.org/Tables/fundomain/ 
6. Singh, Simon. Fermat's enigma: The epic quest to solve the world's greatest mathematical problem. Anchor, 2017.(a gripping historical note on the Fermat's last theorem) 
7. Hyperbolic geometry lecture notes, Charles Walkden
8. Wikipedia 
9. Mathematics Stackexchange
   
10. https://www.cantorsparadise.com/modular-forms-explained-e8e34b33b213
11. https://youtube.com/playlist?list=PLnNqTHlK5sGJ7JOdRY7Cx8d2lnNlyLCYS
12. Hartshorne, Robin. Geometry: Euclid and beyond. Springer Science & Business Media, 2013.
13. Martin, George Edward. The foundations of geometry and the non-Euclidean plane. Springer Science & Business Media, 2012.
14. https://math.stackexchange.com/questions/4655477/connections-between-modular-forms-and-hyperbolic-geometry 
15. https://kconrad.math.uconn.edu/blurbs/grouptheory/SL(2,Z).pdf
    

Image credits

1. Lowry-Duda, David. “Visualizing modular forms.” ArXiv abs/2002.05234 (2020): n. pag.
2. https://mcescher.com/wp-content/uploads/2020/08/CS14-web.jpg
3. https://math.stackexchange.com/questions/1760012/how-to-graph-in-hyperbolic-geometry
4. Diamond, Fred, and Jerry Michael Shurman. A first course in modular forms. Vol. 228. New York: Springer, 2005.
5. Murty, M. Ram, Michael Dewar, and Hester Graves. Problems in the theory of modular forms. Springer Singapore, 2016.
6. Silverman, Joseph H. The arithmetic of elliptic curves. Vol. 106. New York: Springer, 2009.
7. Computing dimensions of spaces of modular forms, Robin Visser

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.